Know Your Market Volatility, a Complete Guide to HV and IV

When trading options for profit, a rule of thumb is to sell options when the Implied Volatility is high, and buy options when the IV is lower.

But do you know what market volatility represents in general and how differences in volatility can affect options prices?

In this article, we'll try to provide an in-depth explanation of what is market volatility, because a solid understanding of volatility is important to trading options for consistent income. We also share the differences between Historical Volatility (HV) and Implied Volatility (IV).

What Is Volatility?

Volatility is the fluctuations and dispersion of data points, and we can use it to indicate the fluctuation of stock prices in the market. Mathematically speaking, volatility is the deviation of the data dispersion.

Thinkorswim shares various market volatility data in the Options Statistics. The most important of them all are Historical Volatility (HV) and Implied Volatility (IV).

What Are the Differences Between HV and IV?

HV is the backward-looking volatility of the underlying, while IV is forward-looking for the theoretically expected future moves.

How to Calculate Historical Volatility?

In case you have left your high school years long behind you, we’ll take it step by step through the process of calculating volatility.

Let us use a recent data set of closing prices of BABA to calculate the volatility. Such backward-looking determination of volatility is commonly known as Historical Volatility (HV).

We first calculate the daily changes of 10 recent BABA closing prices.

Trading days	Last	Daily change
10/4	139.63
10/5	143.14	2.5%
10/6	144.10	0.7%
10/7	156.00	8.3%
10/8	161.52	3.5%
10/11	163.95	1.5%
10/12	163.00	-0.6%
10/13	167.40	2.7%
10/14	166.78	-0.4%
10/15	168.00	0.7%

The standard deviation of these 10 daily changes is 2.54%

Since there are around 252 trading days each year, we can transform the 2.54% standard deviation into an annualised number of 40.3%, which is HV.

Then we can compare our HV number with the Thinkorswim HV data.

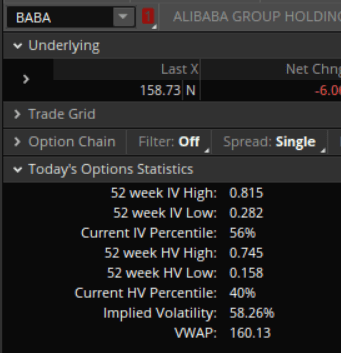
We deduce the Thinkorswim HV from the HV Percentile formula to get a similar number to our calculated HV.

The famous Gaussian normal distribution describes the random outcomes of a data set in our real world where 50% of all outcomes fall on the left side of the mean and the other 50% on the right side of the mean.

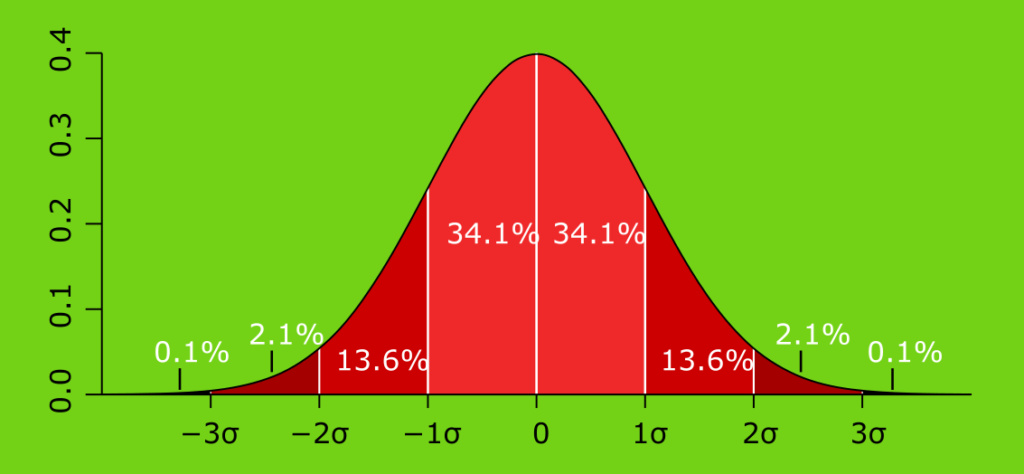
1 standard deviation (σ) on either side of the mean mark the range in which 68% of all fluctuations of the given process would fall. While +/-2σ mark the probability of 95%.

The current closing price for BABA is $158.73, while HV is 40%. So we have a 68% confidence that BABA closing prices will stay within $95.24 and $222.22 in the following year.

If BABA’s closing prices fluctuated more with a bigger standard deviation, its HV would be high.

If the closing prices fluctuated less with a smaller standard deviation, the HV would be low.

How Does IV Affect Options Prices?

Option prices are a function of IV, which is the expected move of the underlying. IV is also calculated from the options pricing model.

Options provide us with rights to sell or buy an asset at a certain price. Such right is inherently associated with a certain cash inflow or outflow and has to be discounted by interest and dividends.

The famous Black Scholes option pricing model was rewarded with a Nobel Prize and provides us with a set of elaborate formulas that allows us to calculate Call and Put option prices. It uses a log-normal distribution model because the price can't go lower than 0, and has a long tail as prices approach infinity.

Call and Put option prices are calculated as follows:

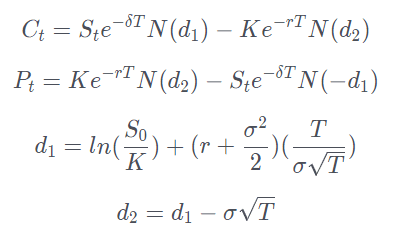
• σ = IV
• δ = dividends
• S = stock price
• K = strike price
• r = risk-free interest rate
• T = time to expiration (year)
• N = normal distribution
• N(d₁) = the expected value of cash/stock inflow if option expires ITM
• N(d₂) = the probability the option expires ITM

Let us calculate the value of AAPL $150 ATM Call option that expires in 39 days. We can use the Option Chain from Thinkorswim to validate our calculations.

• σ = 22.38%
• S = $151.28
• K = $150
• r = 0.04%
• T = 39/365 = 0.106849
• d₁ = 0.153314
• d₂ = 0.080158
• N(d₁) = 0.56
• N(d₂) = 0.53
• C(39) = $5.05

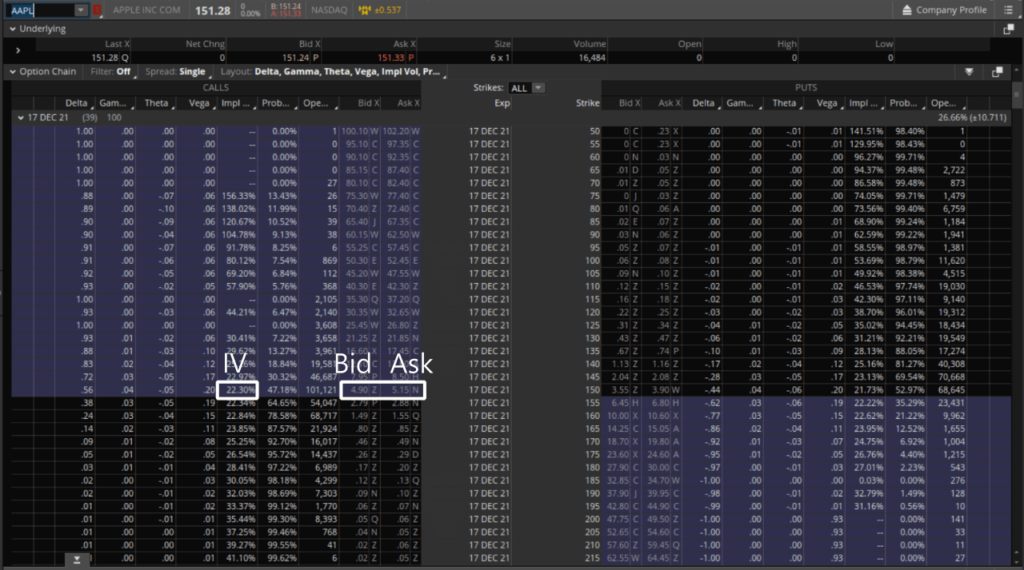
As you may notice, the calculated option price of $5.05 is between the bid price of $4.90 and the ask price of $5.15 shown in Thinkorswim.

So IV and option prices, which comes first?

The Market Maker collects all order flows from brokers, such as TD Ameritrade, Firstrade, Interactive Brokers, then derive ATM option prices based on the increase and decrease of supply and demand for Put and Call options as well as the underlying itself.

Once, you have the ATM options price, you can calculate the IV based on the option pricing model. We have to do some trial and error to approximate the IV value to match the AAPL Call price.

IV	Call prices
10%	2.67
30%	6.56
50%	10.47
70%	14.37
90%	18.27

We see the IV between 10%-30% give results closest to $5.05.

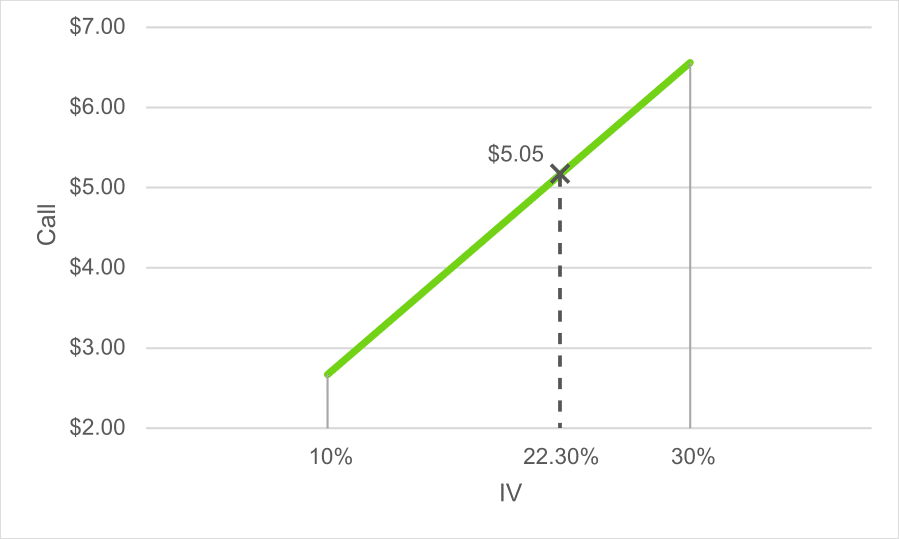
We interpolate the IV between 10% and 30% to find the correct IV as 22.30%, which is the market expectation of future price moves.

Find High Probability Iron Condor Trades Using IV

Now you have a better understanding of how volatility and options prices relate to each other. You can use the Options Scanner to find high probability Iron Condors to sell during high IV, and buy to close at low IV.

• We want to choose opportunities with greater than 30 DTE to get the safest theta decay and less gamma.
• We can filter IV Perc >67% to find opportunities that have a high chance of contracting IV and vega in our favour.
• By choosing Market Cap ($B) larger than 10 billion, we avoid choosing stocks that can get manipulated and explode like AMC.
• A good idea is to eliminate stocks with depressed price movement, or in Squeeze, because IV will expand soon after.
• We should also avoid underlying that have an upcoming Earnings Date in 30 days to reduce the chance of large fluctuations.
• Finally, we can sort the Iron Condor ROC by descending order to get a shortlist of highest return Iron Condors.

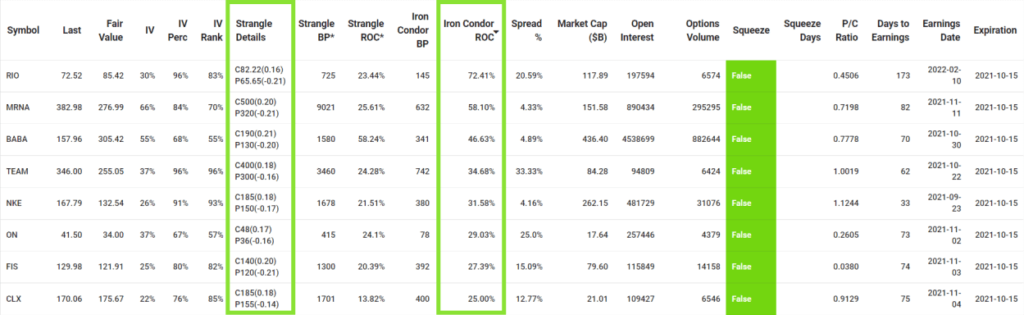
We can use the Options Volume in the watchlist to find more liquid options opportunities. In the list of high return Iron Condors, MRNA has greater Options Volume than RIO, so we get better fills when entering and exiting trades. Let's trade an Iron Condor for MRNA.

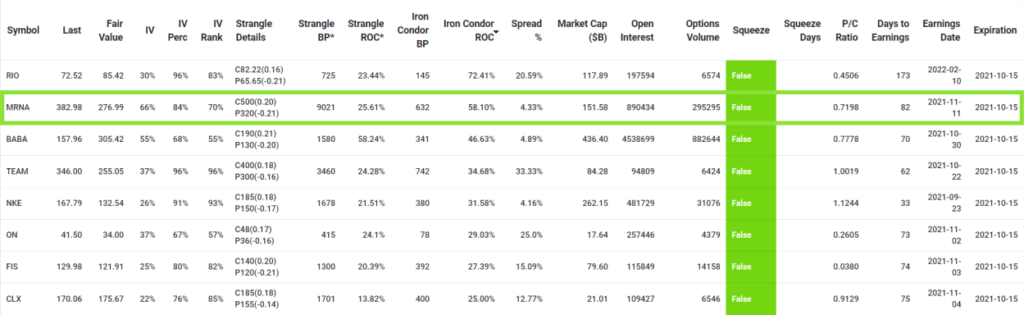
When we sell an MRNA Iron Condor that expires in 54 days, if the MRNA stock price does not exceed the short Put and short Call strike prices, we can make 58% maximum profit when the 4 options expire worthless.

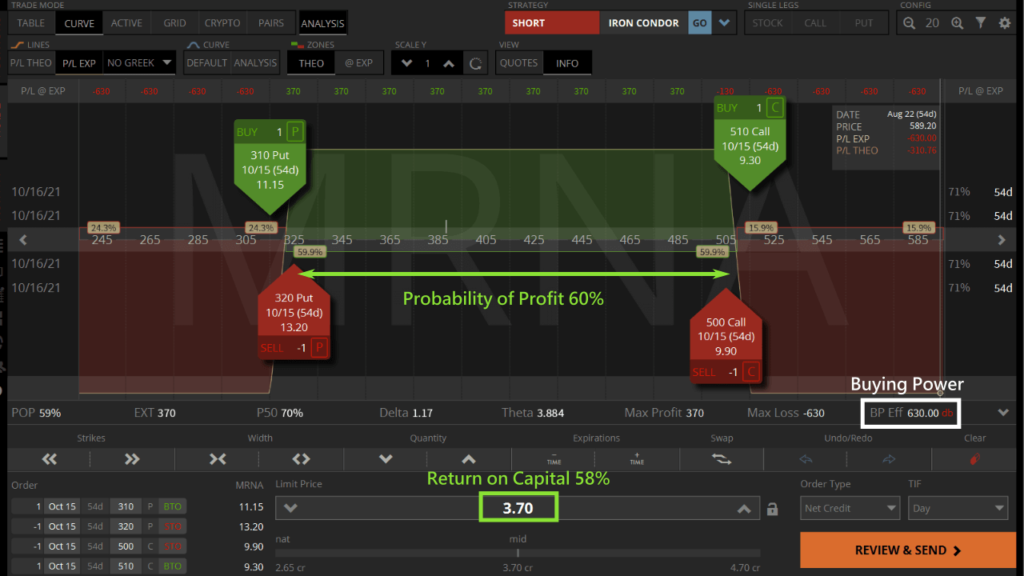
Now you know how to use the Options Scanner to filter the best Iron Condor stocks to trade. Remember to use the scanner often to find high return neutral trades to sell, and profit from the lack of price movement.

Trending Articles